动起来 比起来

——《有余数的除法》教学设计中的两点微创新之处

  张林辉

陶行知先生有过一个精辟的比喻：“接知如接枝。”他说：“我们要以自己的经验做根，以这经验所发生的知识做枝，然后别人的知识方才可以接得上去，别人的知识方才成为我们知识的一个有机部分。”任何有效的教学都始于对学生已有经验的充分挖掘和利用。把零散肤浅的生活经验纳入个体的意义建构中进行同化顺应，纳入到自己的认知结构中去，从而学得轻松、学得有趣、学得深刻。
  《有余数的除法》是人教版小学二年级下册的教学内容，学生在学习的过程中往往只是表面的知道了什么样的数是余数以及余数与除数的关系，并未真正领会余数的涵义以及知识间的内在联系。为此，在教学上做一些细节的设计想方设法让学生“动起来”、“比起来”，这样，学生对知识的理解、把握就水到渠成。

一、动起来，见“树木”更要见“森林”，得以窥见全貌，系统地建立知识结构

【教学设计】

未知的苹果个数，动态地、分层地展示平均分的过程。

1.课件出示一堆苹果（个数未知），把它们平均分到3个盘子里，问是刚好分完呢？还是有剩余的？

2.动态展示课件，让学生猜一猜——可能刚好分完（没有余数），也可能有剩余的（有余数）。

3.引申：如果是没有余数，可能是哪些算式？顺势复习表内除法。

4.再次引申：如果有余数，可能是哪些算式？课件动态展示（一共14个），让学生觉得能判断有余数的时候可以喊“停”，如发现：7÷3=2……1（个）

5、形成下面的结构图示。

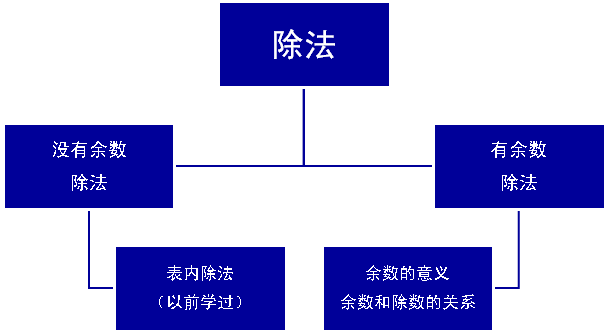
【设计意图】

数学教育专家弗赖登塔尔曾说 : “没有一种数学思想，以它被发现时的那个样子公开发表出来． 一种问题被解决后，相应地发展成一种形式化的技巧，结果把求解过程丢到一边，使火热的发明变成了冰冷的美丽。”数学中有很多“规定”汇聚了几代人的智慧结晶，具体到教材中，往往呈现为简短的几行字，看上去只有“冰冷的美丽”。比如说：余数的概念以及它是怎样来的？但是作为教师，我们可以创设有温度的生动情境，将这种“冰冷的美丽”还原为学生们的“火热的思考”。

这个教学环节不是以知识定论的形式呈现学习内容的教学，因为那样看似逻辑清晰、快捷高效，但它对学生来说，一是缺乏背景知识的了解，二是缺乏认知的挑战性。引导学生接受新的概念并非“一蹴而就” ，这特别需要教师要有前后联系的意识，这个教学环节抓住新旧知识之间的联结点，将“有余数除法”和“没余数除法”进行有机地衔接——正因为苹果个数是未知的，待定的，才有猜测的必要，才能很自然地把平均分的两种可能性很自然地引出来。我的做法是让课件动起来，思维动起来：未知的苹果个数，动态地、分层地展示平均分的过程，目的是把静态、抽象的余数概念化身为动态的、形象直观且充满童趣的学习材料，使封闭单一的思维方式变得开放、发散。使学生在这样的问题情境中，经历某种智力的探险。“最好的老师是把学生托起来，而学生还以为是自己站得高呢。” 

二、比起来，重经验更要重体验，经历关键步子，完整地体验产生过程

（一）“余下的数”与“余数”的对比，体验余数产生的过程。

【教学设计】

1、7÷2=16……5   分了一次，余下的数是5,5是余数吗？ 5＞2，每盘还够一个，因此5叫“余下的数”，还不是真正的“余数”。

2、7÷2=2……3 分了2次，余下的数是3,3是余数吗？——3＞2，每盘还够一个，因此3叫“余下的数”，还不是真正的“余数”

3、7÷2=3……1  分了3次，余下的数1，1是余数吗？——1＜2，每盘不够一个了，因此1叫“余数”（每盘不够一个了，也就是解决余数为什么要小于除数的问题），只有这样的数才叫余数。

【设计意图】

1.找准认知障碍，为学生真正解困。

教学要瞄准学生认知障碍，想学生所想，急学生所急，找准学生的困惑之处，真正需要之处。学习有余数除法时，学生有个似是而非的概念：在一步一步平均分的过程中，从第一次到最后一次，每一次都会有剩余的，引发认知冲突：三次平均分，都有余下的数，到底哪个才是数学意义上的“余数”？其他为什么不是？为什么余数要比除数小呢？所以从这个意义上来说，要经常给学生找麻烦“先问迷糊，再教明白”，先乱后治。知识和思想只有在学习的“阵痛”之中产生出来,这样才有价值，才能留下深刻的印象。否则，轻易得到的也就会轻易地失去。

这个教学环节，目的是适度拉长体验过程，于精妙处当慢则慢。增加“悟”的时间，长时间的“悟”，然后是有所体验、有所心得、有所发现。

2.提供结构化素材，方便进行对比思辨。

所谓 “由近及远 ，瞻前顾后”，是指在教学时 ，教师要考虑所教知识的 “来龙去脉 ”。由于数学知识结构严谨 ，教材编排大多以螺旋式上升的方式相互承接 ，而教材结构不会自动成为学生的知识结构 ，需要教师对材料进行有效设计，并在课堂上适度引导 ，才能为后续的学习积累有效的活动经验。

本环节用简单但富有结构的材料,通过层层设问、有效追问,逐步引导孩子初步建构余数的概念，了解余数这个知识在整个体系中的位置与其他知识的相互“关系”。

求比、求思、求连是本设计的初衷。

求比，注重引导学生在平均分的进程三种不同情况下进行有效的比较。

求连，注重各知识之间的连接，如剩余的数和余数，似是而非，在不断地进行辨析。

求思，问题的“卷入度”比较高，结构化的素材引领着学生不断思考。

3.运用“反向厘析”，在“破与立”之间中不断地思辨。

     操作不等于探究，动手不等于动脑。

“正”和“反”是事物存在的两个方面，也是人们认识事物的两个角度和两种方式。在数学课堂教学中，“正面强化”也正是从数学概念、原理、方法的本质内涵的正面出发，通过对教学要点的不断强化，以达到加深印象、增强理解、把握内核的教学实效；而“反向厘析”，则是从结果、从反面出发，通过推理、辨析、比较等思维活动，不断凸显数学概念、原理、方法的本质要义，从而达到教学的有效。本教学环节，就利用“反向厘析”，展现了几个“余下的数”来干扰学生，有利于增强对错误的免疫力。

这个环节有破有立，在“余数与非余数”之间不断地“破——立”，不断地思辨，建立“余数”的概念。“破”与“立”的思辨中有了深刻的体验，所以才使这个环节变得非常有张力。

（二）巧妙对比，深入理解知识间的联系。

1、算式与摆法的比对，“物”“式”对应。

【教学设计】

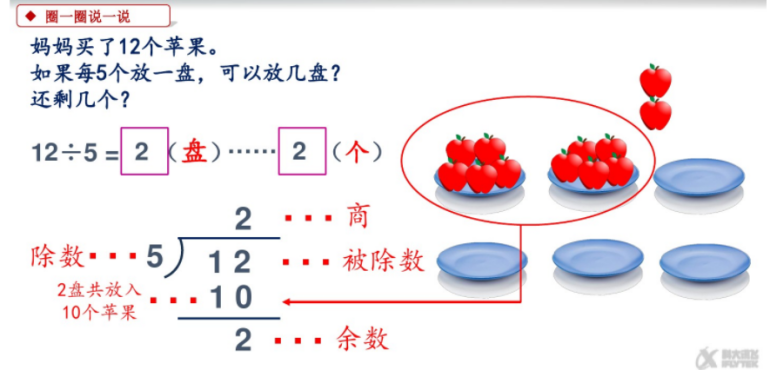
【设计意图】

各部分的意义与竖式比对，更加深刻地理解概念的本质意义。

2、商和余数是同一个数字，对比其意义。

【教学设计】

变式练习，求“商”与求“余数”的对比辨析：

（如上图）这两个2，意义一样吗？

【设计意图】

在具体的算式中，体会它们的意义是完全不同的。

3、两个有关联的算式进行比对，在除数相同的情况下，余数之间的关系对应被除数之间的关系。

【教学设计】

【设计意图】

乌申斯基：比较是一切理解和一起思维的基础。同中求异识区别，异中求同找联系。这组题的设计，目的在于一是让学生能迅速找到合适的商，二来发现上下两题被除数之间的关联性。

比如：第一题，因为5比4多1，所以余数比0多1；

比如：第三题，因为23比24少1，所以余数比3少1，为2。

托尔斯泰说：“优秀的艺术构思，应该有这样一个点，所有光会集中到这一点上，或从这一点放射出去。”在《有余数的除法》教学时，由于关注了这样的几个点，学生在不断地感悟中发现问题、解决问题，从而自然地获取数学知识。

                       （本文2019年发表在《德阳教育》）

                       作者单位：德阳外国语学校小学部  618000